[强化学习]价值学习

定义

$U_t$ = $R_t + \gamma · R_{t+1} + \gamma ^ 2 · R_{t+2} + … \gamma ^{n - t} · R_n$.
其中$U_t$为Return,$\gamma \in $ [0,1]为折扣率。$U_t$以来于从t时刻开始的所有动作和状态，未来的动作A和状态S都是随机变量，因此$U_t$也是随机的。我们对$U_t$求期望就可以排除掉随机性。动作价值函数 的定义为

$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t\mid S_t=s_t,A_t=a_t]$$

最优动作价值函数 用最大化消除策略π:

$$Q_{\star }(s_t,a_t)=\underset{\pi }{max}{Q}_{\pi }(s_t,a_t),\mathrm{\forall }{s}_t\in \mathcal{S},a_t\in \mathcal{A}.$$

可以理解为已知$s_t$和$a_t$，不论未来采取什么样的 策略π ，回报$U_t$ 的期望不可能 超过 $Q^*$。简单的说就是Agent根据$Q^*$函数的期望来选择价值最高的动作。

DQN

简介

DQN是 一种价值学习的方法，利用一个神经网络Q(s,a;w)来近似$Q^*$(s,a)。神经网络的参数是w，输入是状态s，输出是很多数值a，这些事神经网络对每个动作的打分，通过奖励来寻训练神经网络。

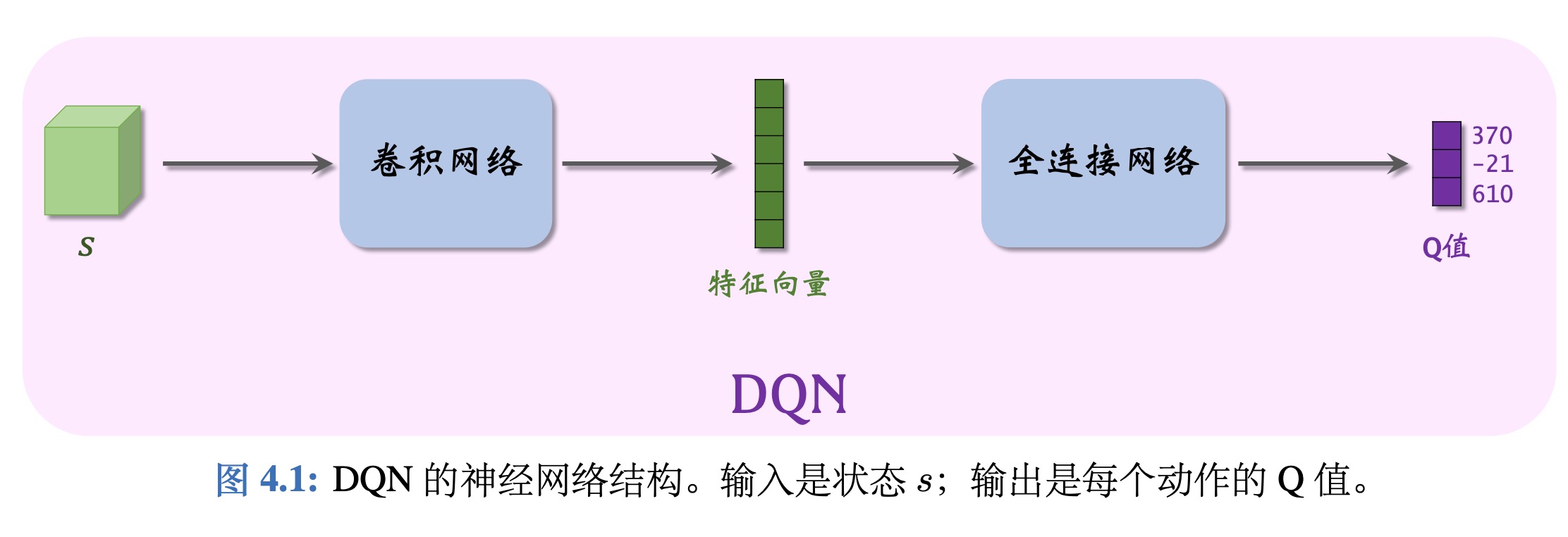
举个例子，动作空间是 A = {左, 右, 上}，那么动作空间的大小等于 |A| = 3，那么 DQN 的输出是 3 维的向量。由于上的得分(610)最高，所以Agent应该选择上这个动作。

利用DQN玩游戏的过程

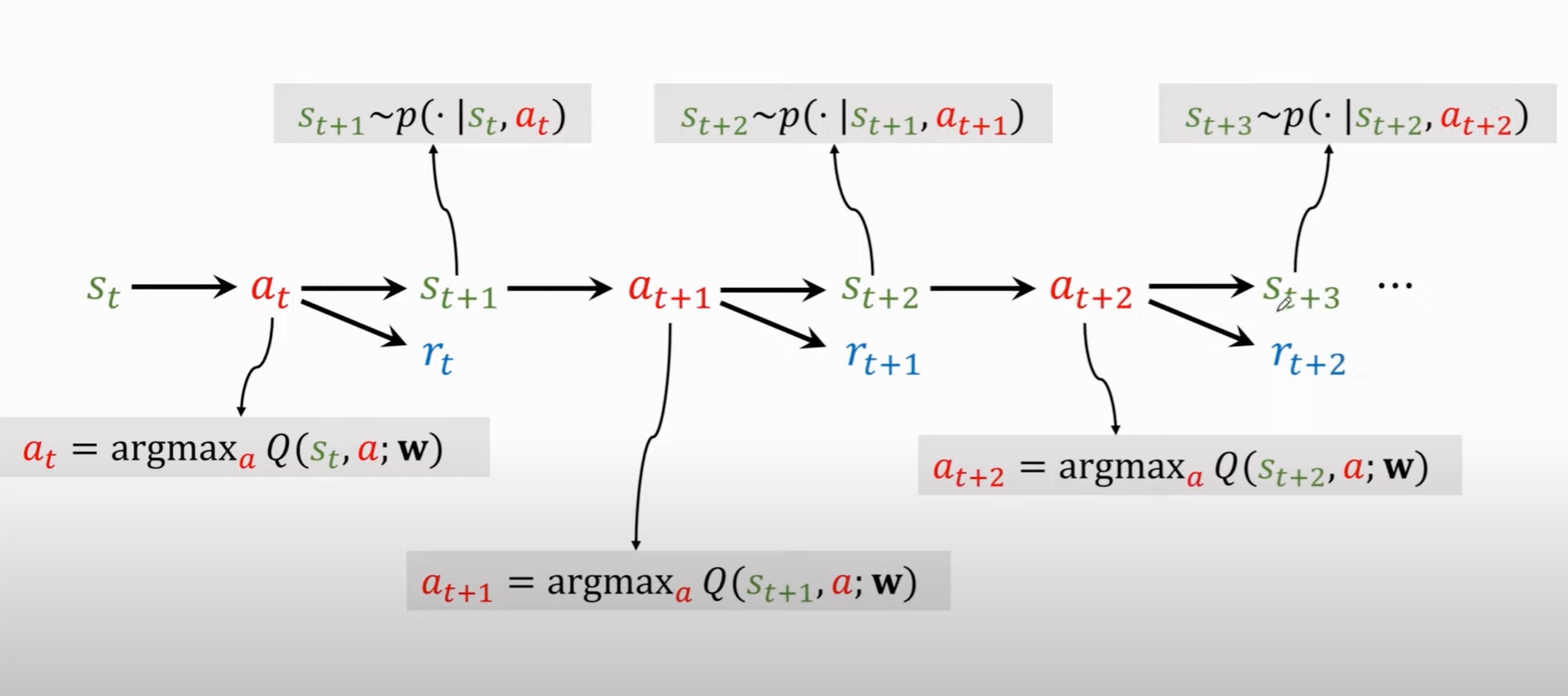
DQN的梯度

在训练 DQN 的时候，需要对 DQN 关于神经网络参数 w 求梯度。

$${\mathrm{\nabla }}_{\mathit{w}}Q(s,a;\mathit{w})\triangleq \frac{\mathrm{\partial }Q(s,a;\mathit{w})}{\mathrm{\partial }\mathit{w}}$$

表示函数值 Q(s, a; w) 关于参数 w 的梯度。因为函数值 Q(s, a; w) 是一个实数，所以梯度的形状与 w 完全相同。

我们一般使用TD算法来训练DQN

原始的TD算法

Agent观测到当前状态$s_t$并且执行动作$a_t$。
环境给出新的状态$s_{t+1}$并给出奖励$r_t$

• A transition：($s_t,a_t,r_t,s_{t+1}$)
• TD target:

$$y_t=r_t+\gamma \cdot \underset{a}{max}Q(s_{t+1},a;\mathbf{w})$$

• TD error:$\delta _t$ = $q_t$ - $y_t$, where $q_t$ = Q($s_t,a_t$,w)

• goal:使$q_t$更加接近$y_t$。也就是说让TD error尽量小。

• TD learning: L(w) = $\frac{1}{T} \sum_{t=1}^T \frac{\delta ^2}{2}$

• Online Gradient descent：

  • 观察($s_t,a_t,r_t,s_{t+1}$) 求出$\delta_t$
  • 计算梯度:$g_t$ = $\delta_t$* $ \frac{\partial Q(s_t,a_T;w)}{\partial w}$
  • 梯度下降：w <- w - $\alpha $ * $g_t$
  • 丢弃($s_t,a_t,r_t,s_{t+1}$)

缺点：

• 浪费经验:原始的TD算法在做完一个transition就被丢弃不再使用，造成了经验的 浪费，事实上这些经验是可以重复使用的。这就是做“经验回放的主要原因”。
• transitions之间的相关性:我们按顺序使用每一条transition来更新w,前后两条transitions之间有很强的关联,实验证明这种相关性是有害的。如果能把序列打散，消除相关性，则有利于把DQN训练得更好。

“经验回放”可以有效克服刚才提到的两个缺点。

经验回放

• A transition ($s_t,a_t,r_t,s_{t+1}$)
• 存储最近b个transition放在replay buff中：
  
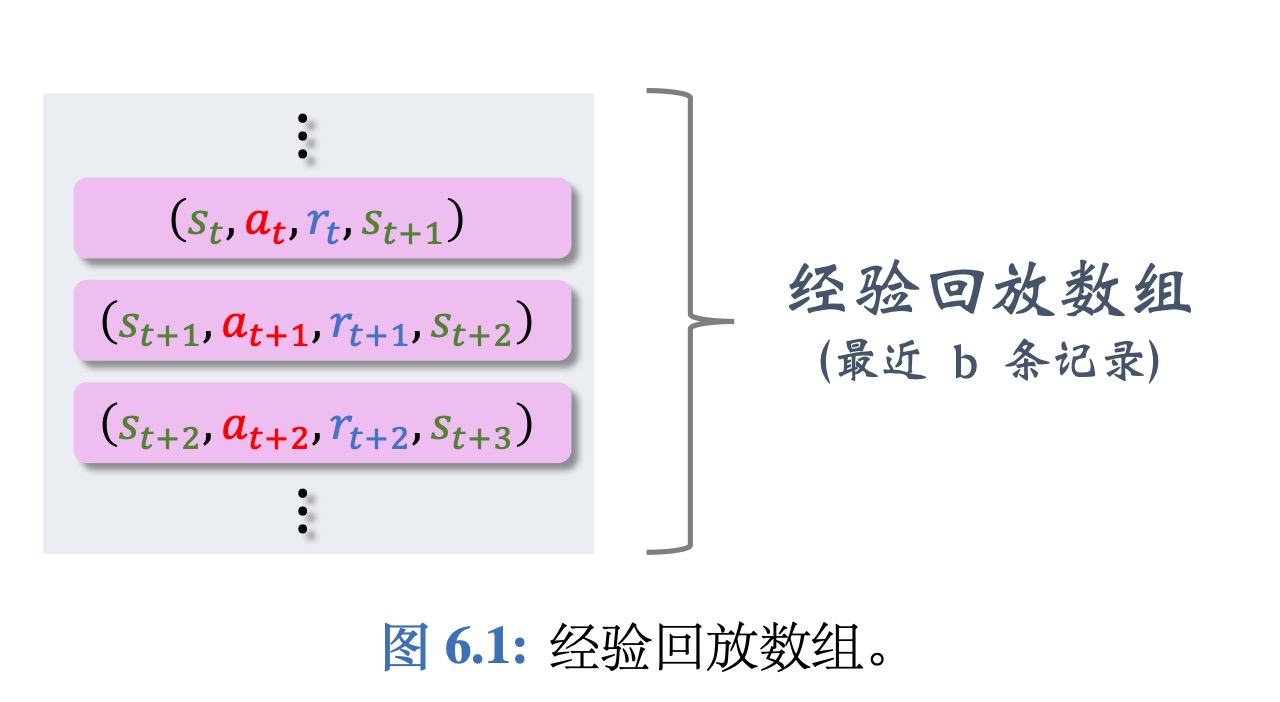
  如果存满了则删除最久的一条transition，放入最新的transition。

优先经验回放

优先经验回放(prioritized experience replay)是一种特殊的经验回放方法，它比普通 的经验回放效果更好:既能让收敛更快，也能让收敛时的平均回报更高。
基本想法是用非均匀抽样代替均匀抽样。两种方法设置抽样概率。

• 一种抽样概率是:

$$p_j\propto \left|{\delta }_j\right|+ϵ$$

此处的ϵ是个很小的数，防止抽样概率接近零，用于保证所有样本都以非零的概率被抽到。

• 另一种抽样方式先对|$δ_j$|做降序排列，然后计算
  $$p_j\propto \frac{1}{\mathrm{rank}(j)}$$
  此处的 rank(j) 是 |$δ_j$| 的序号。大的 |$δ_j$| 的序号小，小的 |$δ_j$| 的序号大。两种方式的原理 是一样的，|$δ_j$| 大的样本被抽样到的概率大。

两种抽样的原理是一样的，TD error越大，transition被抽到的概率就越大。
抽样的概率是不同的，也就是非均匀抽样。这样会导致DQN的预测有偏差，应该相应 调整学习率 ，抵消掉不同抽样概率造成的偏差。这里的 𝛼 是学习率也叫做步长。如果做均匀抽样，所有 transitions 都有相同的学习率。如果做非均匀抽样的话，应该根据抽样概率来调整学习率。如果一条 transition 有较大的抽样的概率，那么应该把它的学习率设置得较小

• 计算 𝑛 乘以$𝑝_𝑡$，求负𝛽次幂$(np_t)^{-𝛽}$把它乘到学习率上.𝛽$\in$[0,1]
• 在均匀抽样下，抽样概率$p_1,..,p_n = \frac{1}{n}$ ,在这种情况下所有的n乘以$p_t$都等于1，不会影响学习率。
• 如果是非均匀抽样，$𝑝_1$ 到 $𝑝_n$各不相同，于是学习率会有所不同。对于概率较大的$𝑝_𝑡$，算出来的幂较小，会让学习率变小，反之亦然。
• 𝛽是个超参数，需要调参。论文里建议一开始让 𝛽 很小，然后逐渐让 𝛽 增长，最终增长到1。

---

• 为了做“优先经验回放”，要把每一条transition 都标记上 TD Error$𝛿_𝑡$，$𝛿_𝑡$决定了这一条 transition 的重要性，决定了它被抽样的概率。
• 如果一个transition刚刚被收集到，还没有被用来训练DQN，我们不知道它的$𝛿_𝑡$：
  • 我们就把它的$𝛿_𝑡$设置为最大。
  • 给予它最大的权重。
• 在训练 DQN 的同时，要对$𝛿_𝑡$做更新。每次我们使用一条 transition 的时候，我们要重新计算它的$𝛿_𝑡$,这条 transition 就有了新的权重。

总结

高估问题

用TD算法训练DQN，会导致DQN高估真实的动作价值。

高估的原因：
•最大化:是计算 TD target 用到了最大化，它会导致高估
•Bootstrapping:如果当前 DQN 已经出现高估，下一轮的 TD target更会高估，再进一步推高DQN的输出,一步步让DQN的高估越来越严重。

最大化

数学解释

• 设$𝑥_1,..,𝑥_𝑛$为任意 n 个观测到的实数.
• 在$𝑥_1,..,𝑥_𝑛$中添加均值为零的随机噪声，将得到的输出记为$𝑄_1,..,𝑄_𝑛$
• 由于噪声的均值等于零，噪声不会影响 Q 的均值,我们可以得到Q的均值求期望，结果就等于x的均值:
  $\mathbb{E} [mean_i(Q_i)]= mean_i(x_i)$
• 但是噪声会让最大值增长，Q的最大值往往大于x的最大值,对Q的最大值求期望，结果一定会大于等于x的最大值:
  $\mathbb{E} [max_i(Q_i)] ≥ max_i(x_i)$
• 同样的道理，随机噪声会让最小值变得更小,Q 的最小值往往会小于 x 的最小值:
  $\mathbb{E} [min_i(Q_i)] ≤ min_i(x_i)$

在DQN中

• 设 $𝑥(𝑎_1),..,𝑥(𝑎_𝑛)$为真实的动作价值,$𝑎_1,..,𝑎_𝑛$是动作空间中所有的动作。
• DQN的估算价值为：$𝑄(𝑠, 𝑎_1;𝐰),..,𝑄(𝑠, 𝑎_𝑛;𝐰)$。
• 假设没有误差，同理有:
  $\mathbb{E} mean_a(x(a))= mean_a𝑄(𝑠, 𝑎;𝐰)$
• 计算TD target的时候，要对DQN关于动作a求最大化，把结果记做q = $max_a𝑄(𝑠, 𝑎;𝐰)$,之前我们分析过，往 x 里面加噪声，然后求最大化，得到的结果会高估 x 的最大值.同理也有
  q ≥ $max_a(x(a))$

求最大化使得 TD target 大于真实价值，因此导致 DQN 高估

Bootstrapping

在强化学习中，Bootstrapping的意思是“用一个估算去更新同类的估算”，也就是自己把自己举起来。例如在TD算法中，我们为了更新DQN咋t时刻的预测，用来DQN在t+1时刻做出的预测。就算是Bootstrapping。

• TD中的Bootstrapping
  • TD target用到了DQN在t+1时刻的估计值$q_{t+1} = max_a Q (s_{t+1},a;w)$。
  • 我们拿 TD target 来更新 DQN 在 t 时刻的估计，这就是用 DQN 来更新 DQN 自己，所以叫做Bootstrapping
• 假设DQN已经高估了动作价值。
• 那么Q($s_{t+1},a,w$)也是一个高估。
• 最大化$q_{t+1}$也会被高估，进一步推高高估价值。
• 拿$q_{t+1}$计算 TD target，再更新DQN,这样高估又被传播回 DQN，让DQN的高估变得更严重。

高估为什么有害

DQN输出的动作价值，Agent选择价值最大的动作执行。这个决策根据的是 相对大小 而不是绝对大小。

高估本身不是问题，只要高估是均匀的就好。
假设三个动作的价值：a = 200,b = 100, c = 230
如果高估是均匀的，那么对决策不会产生影响。如果高估是非均匀的，有的动作被高估一点，有的则被高估很多，DQN的输出变成了
a = 280,b = 300,c = 240。这样的价值就产生了误导，会做出错误的决策。

实际上DQN的高估是非均匀的，如果一个transition在replay buffer里出现的越频繁，高估就越严重。（每次更新都会造成一次高估 ）

解决高估的方法

• 避免 Bootstrapping：不要用 DQN 自己算出来的TD Target来更新 DQN，而是用另一个神经网络来计算TD target，另一个神经网络被称作 target network ，目标网络。

• Double DQN：用来缓解“最大化”造成的高估。Double DQN 也用 target network，但是具体用法有一点点区别。

  Target Network

  用两个神经网络,第二个神经网络叫做 target network。

  • Taregt Network:Q(s,a;$W^-$)
    • 与DQN有相同的网络结构，Q(s,a;w)。
    • 不同在于参数$w^-$ ≠ w。
  • DQN,Q(s,a;w)用来控制Agent，并收集经验，经验为多条transition{($s_t,a_t,r_t,s_{t+1}$)}。
  • Target Network,Q(s,a;$w^-$)唯一的用途是用来计算TD target。$$y_t=r_t+\gamma \cdot \underset{a}{max}Q(s_{t+1},a;\mathbf{w–})$$

用在TD算法上

• 使用transition($s_t,a_t,r_t,s_{t+1}$)来更新w。

  • TD target：$y_t=r_t+\gamma * \max_a (s_{t+1},a;w^-)$ （这里用的是Target Network中的参数$w^-$）
  • TD erroe:$\delta _t$ = $q_t$ - $y_t$, where $q_t$ = Q($s_t,a_t$,w)
  • SGD: w <- w - $\alpha $ $\delta_t$ $ \frac{\partial Q(s_t,a_T;w)}{\partial w}$ (这里只更新DQN中的参数w，不更新TargetNetwok的参数)

• Target Network中的参数$w^-$需要隔一段时间更新:

  • 方式一:直接拷贝DQN中的参数w。 $w^-$ <- w
  • 方式二:做加权平均。$w^-$ <- $\tau$ w + (1 - $\tau $) $w^-$

• 比较

  • DQN自己更新：$y_t=r_t+\gamma * \max_a $($s_{t+1}$,a;w)
  • Target Network更新：$y_t=r_t+\gamma * \max_a $($s_{t+1}$,a;$w^-$)

用 target network 会减小DQN高估的程度,让DQN表现得更好,但还是无法避免高估。即使用了 target network，也还有最大化操作，仍然会让 TD target 大于真实价值,除此之外，target network会用到DQN的参数，target network 无法独立于 DQN,所以无法完全避免 bootstrapping。

Double DQN

TD Target：$y_t=r_t+\gamma * \max_a $($s_{t+1}$,a;$w$)
将TD target的公式拆成两步:

• 在DQN中,选出能最大化 Q 函数的动作，记为$a^*$: $$a^{\star }=\underset{a}{\mathrm{argmax}}Q(s_{t+1},a;\mathbf{w})$$
• 然后再Target Network中计算 TD target:$$y_t=r_t+\gamma \cdot Q(s_{t+1},\mathrm{a*};\mathbf{w-})$$

不同于前面的原始DQN和Target Network都是在自己的网络中计算最大值和求Target Network。

我们可以知道：
Q($s_{t+1,a^*;w^-}$) ≤ $\max _a Q(t+1,a;w^-)$

比较

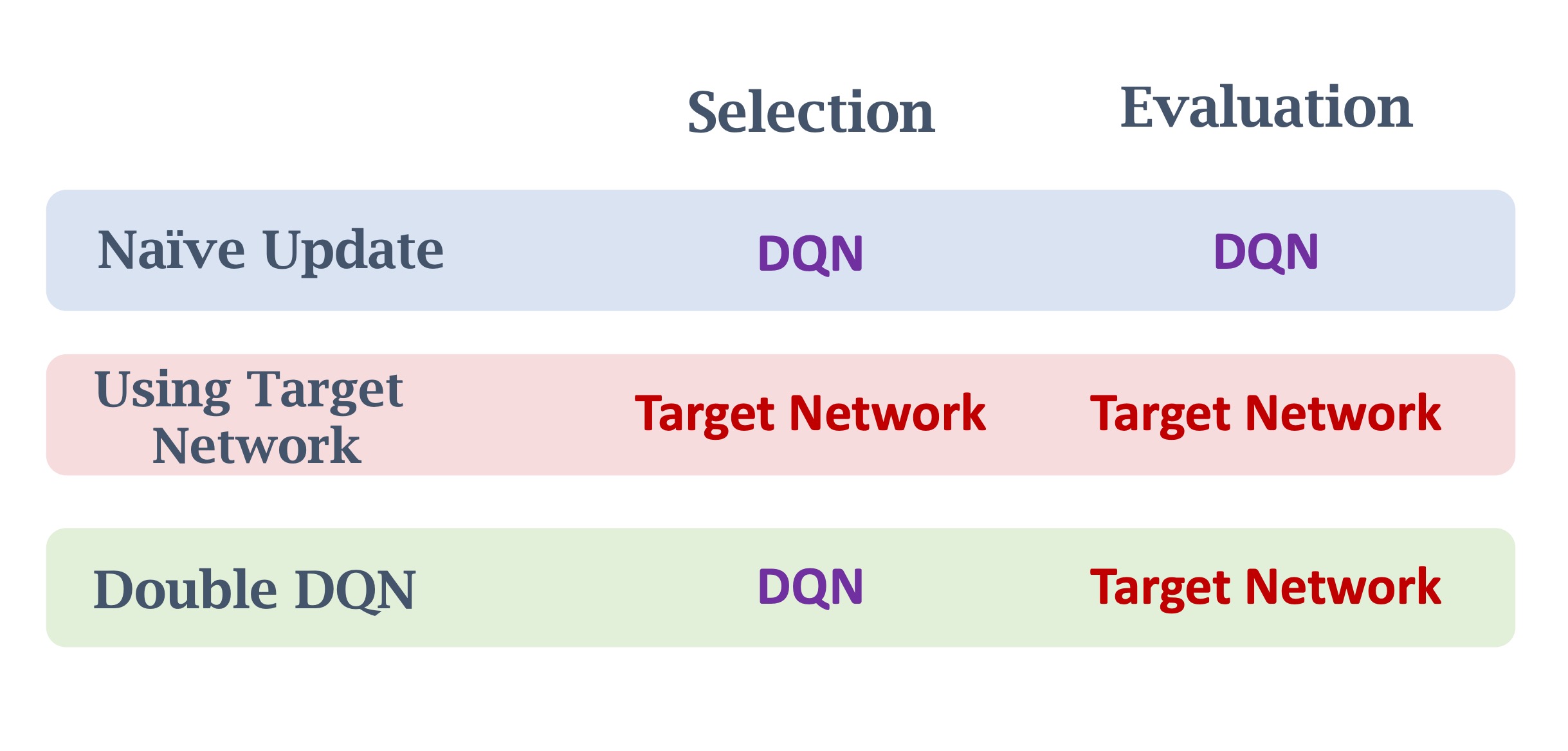
Dueling Naetword

网络结构

• 最优动作价值函数:$Q^{\ast}(s,a)=\max_πQ_π(s,a)$.
• 最优状态价值函数:$V^{\ast}(s)=\max_πV_π(s)$.
• 优势函数:$A^{\ast} (s,a)=Q^{\ast}(s,a)-V^{\ast}(s)$.

优势函数的意思是动作a相对于baseline的优势。

• 定理1:$V^{\ast}(s)=\max_aQ^{\ast}(s,a)$
• 由（1）可知:$\max_a A^{\ast}(s,a)=\max_aQ^{\ast}(s,a)-V^{\ast}(s)=0$.
• 变化优势函数的定义可以得到:$Q^{\ast}(s,a)=V^{\ast}(s)+A^{\ast}(s,a)-\max_aQ^{\ast}(s,a)$.

• 构建网络:
  

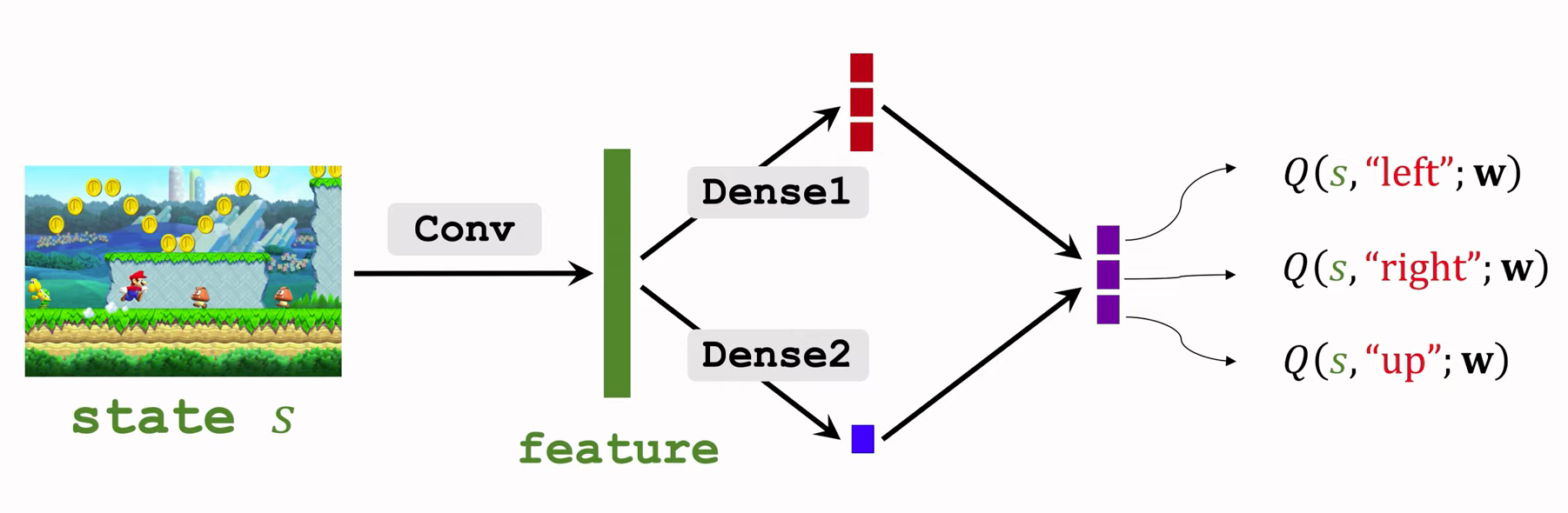
训练过程和DQN网络一样。

解决唯一性问题

• 公式1:$Q^{\ast}(s,a)=V^{\ast}(s)+A^{\ast}(s,a)$.

• 公式1缺点：无法通过学习$Q^{\ast}(s,a)$，来唯一确定$V^{\ast}(s)$和$A^{\ast}(s,a)$。
  • 让$V^{‘}=V^+10$和$A^{‘}=A^-10$。
  • 那么$Q^{\ast}(s,a)=V^{\ast}(s)+A^{\ast}(s,a)=V^{‘}(s)+A^{‘}(s,a)$.
  • 得到的结果不唯一。
  • 不唯一会导致神经网络不稳定，训练不好。
• 公式2:$Q^{\ast}(s,a)=V^{\ast}(s)+A^{\ast}(s,a)-\max_aQ^{\ast}(s,a)$可以避免不唯一性。
• $Q^{\ast}(s,a)=V^{\ast}(s)+A^{\ast}(s,a)-meanQ^{\ast}(s,a)$效果更好。